Calibration Access and Data Handbook



Next: Calling Parameters
Up: CAL_rgsgetXRTFigure
Previous: CAL_rgsgetXRTFigure
Contents
This provides the shape of the XRT along the dispersion direction
(integrated in cross-dispersion).
This function can have two modes of operations:
- Numerical integration of the parameterized PSF (see HIGH
accuracy level described in section 3.2.1)
This parameterization is numerically integrated along the
cross-dispersion direction.
- Dedicated parameterization
A dedicated set of parameters is provided that describes the PSF
when integrated on the cross-dispersion direction. Gaussian and
Lorentzian functions and a linear combination are allowed. The
Gaussian parameterization has the form
with the parameters 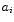 ,
, 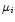 , and
, and 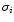 provided by the
CCF per Gaussian.
Lorentzian parameterizations have the form
provided by the
CCF per Gaussian.
Lorentzian parameterizations have the form
with the parameters 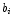 ,
, 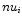 , and
, and 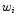 provided by the CCF per
Lorentzian.
provided by the CCF per
Lorentzian.
The functions are selected by a flag in the CCF. The parameters of
the centers (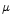 and
and 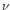 ) are given with respect to a common
center to allow for an assymetric parameterizations. The common
center
) are given with respect to a common
center to allow for an assymetric parameterizations. The common
center 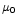 is calculated by
is calculated by
The value of the input argument CENTER_CHAN is added to
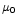 , in order to provide the PSF correctly centered.
, in order to provide the PSF correctly centered.
The width of the PSF of the telescope scales as a function of angle of
incidence on the gratings and diffration angle of the RGA by the
chromatic magnification function 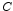 . The chromatic magnification
which is an imaging effect by the gratings that scales the width of
the PSF in the dispersion direction as a function of angle of
incidence and diffraction angle. It is defined as
. The chromatic magnification
which is an imaging effect by the gratings that scales the width of
the PSF in the dispersion direction as a function of angle of
incidence and diffraction angle. It is defined as
and is an input argument.
The function returns the probability distribution 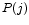 which
calculated from
which
calculated from 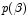 by integration per channel
by integration per channel 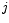
Note: The CAL inverts the parameterization that is in XRT_XPSF along the dispersion axis, because the RGA acts as a
mirorr in this respect.



Next: Calling Parameters
Up: CAL_rgsgetXRTFigure
Previous: CAL_rgsgetXRTFigure
Contents
Michael Smith
2011-09-20
![]() and
and ![]() ) are given with respect to a common
center to allow for an assymetric parameterizations. The common
center
) are given with respect to a common
center to allow for an assymetric parameterizations. The common
center ![]() is calculated by
is calculated by
![]() , in order to provide the PSF correctly centered.
, in order to provide the PSF correctly centered.