Next: 3.5.10 OM specific proposal submission information Up: 3.5.9 OM Operating modes and filters configuration Previous: 3.5.9.5 Multiple rotations of the filter wheel
The choice of a mode or configuration for OM should be driven by a compromise between the time resolution needed and the spatial coverage required for a given pointing. Time discontinuities are due to the overheads (see XRPS User's manual for a detailed description) needed to download the data and configure the instrument for the next exposure.
The full frame modes cover the whole FOV, but they have large overheads.
If time resolution is needed, then windowed modes provide almost continuous
coverage.
The maximum time resolution is achieved in FAST mode (up to 0.5 sec). The
default image configuration, or IMAGE+FAST, allows the user to cover 92% of
the FOV in five successive exposures, obtaining in each of them a small window
(less than 2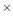 2 arcmin) centred on the pointing attitude and optionally
a FAST mode window (10”.5
2 arcmin) centred on the pointing attitude and optionally
a FAST mode window (10”.5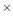 10”.5) centred at the same coordinates.
If one needs time coverage on a larger area, one can make several short
(
10”.5) centred at the same coordinates.
If one needs time coverage on a larger area, one can make several short
(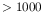 sec) Science User Defined Mode exposures (image window up to
7'.6
sec) Science User Defined Mode exposures (image window up to
7'.6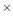 7'.6, if binned). However, for crowded fields, exposures
may be lost, and longer exposure times are encouraged.
7'.6, if binned). However, for crowded fields, exposures
may be lost, and longer exposure times are encouraged.
Field spectroscopy is better achieved using full frame low resolution, while if one wants to monitor spectral variations of the target, there is a pre-defined window configuration for each of the grisms which is optimally located to encapsulate the target spectrum. Be aware, however, of the issue of the impact of degradation due to the Jupiter patch (see section 3.5.3.2).
Examples 1: Imaging
Example 1a: Science User Defined Mode
With 10 ks approved observation time,
two OM exposures with 4 ks each can be defined in Science User Def
mode. The overhead is 0.3 ks per exposure, and one can either cover the
central 5'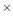 5' at high resolution, or 7'.6
5' at high resolution, or 7'.6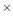 7'.6 at
low resolution (2
7'.6 at
low resolution (2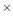 2 binning). The total required observing time
will be: 1.3 ks+2
2 binning). The total required observing time
will be: 1.3 ks+2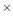 (0.3 ks + 4.0 ks) = 9.9 ks. With
the shortest sensible exposure time of 1 ks, the maximum number of
exposures that can be defined is six:
1.3 ks+6
(0.3 ks + 4.0 ks) = 9.9 ks. With
the shortest sensible exposure time of 1 ks, the maximum number of
exposures that can be defined is six:
1.3 ks+6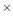 (0.3 ks + 1.0 ks) = 9.1 ks, but note that
significantly more overhead time is needed, and such a setup only
makes sense if multiple filters are needed. For monitoring of expected
variability, please see Example 3. Note, that for best efficiency, the
remaining time (in the last case: 900 sec) can be added to one of the
exposures, e.g., the last of the six exposures can be
defined as 1.9 ks.
(0.3 ks + 1.0 ks) = 9.1 ks, but note that
significantly more overhead time is needed, and such a setup only
makes sense if multiple filters are needed. For monitoring of expected
variability, please see Example 3. Note, that for best efficiency, the
remaining time (in the last case: 900 sec) can be added to one of the
exposures, e.g., the last of the six exposures can be
defined as 1.9 ks.
It is recommended to increase the exposure time of the exposure that uses the filter with the lowest throughput (see Fig. 102).
Example 1b: Standard Imaging Mode
Since an EPIC/RGS image mode exposure consists of
five subexposures, a defined exposure time of, e.g., 1 ks gives a total
exposure time of 5 ks for each 1-ks EPIC/RGS image mode exposure.
The overhead consists of 1.3 ks (overhead times are given with numbers
in italic font) at
the beginning of the observation (including the star tracker acquisition
time) and 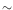 1.6 ks for each exposure. If, for example,
two EPIC/RGS image mode are defined, then the total observing
time needed is: 1.3 ks + 2
1.6 ks for each exposure. If, for example,
two EPIC/RGS image mode are defined, then the total observing
time needed is: 1.3 ks + 2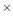 (1.6 ks + 5
(1.6 ks + 5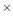 1.0 ks) = 14.5 ks.
The overhead times are added automatically when entering the data in the
RPS tool.
1.0 ks) = 14.5 ks.
The overhead times are added automatically when entering the data in the
RPS tool.
Thus, an approved 10-ks observation allows the definition of only
one EPIC/RGS image mode exposure:
1.3 ks + 1.6 ks + 5 1.0 ks = 7.9 ks. Conversely, only one
filter can be used with this mode. The remaining 2.1 ks can not be used
in this mode, because the overhead of 1.6 ks leaves only 500 sec of exposure, shorter
than the minimum allowed exposure time of 800 sec.
1.0 ks = 7.9 ks. Conversely, only one
filter can be used with this mode. The remaining 2.1 ks can not be used
in this mode, because the overhead of 1.6 ks leaves only 500 sec of exposure, shorter
than the minimum allowed exposure time of 800 sec.
In order to use the full time, one can either use Science User Defined Mode (see below) or increase
the defined exposure time by 2.1 ks/5=0.42 ks, thus with one
EPIC/RGS image mode exposure with an exposure time of 1.42 ks, we
get: 1.3 ks + 1.6 ks + 5 1.42 ks = 10.0 ks.
1.42 ks = 10.0 ks.
Example 1c: Full Frame Low Resolution
If Full Frame Low Resolution Mode is used, in 10 ks we can obtain two
exposures of 1.6 ks each, in two different filters:
1.0 ks + [2 (2.9 ks + 1.6 ks)] = 10 ks (the FF Low Res.
exposure overhead is 2.9 ks). The overhead of the first
exposure of the observation for this mode being
(2.9 ks + 1.6 ks)] = 10 ks (the FF Low Res.
exposure overhead is 2.9 ks). The overhead of the first
exposure of the observation for this mode being  1.0 ks.
1.0 ks.
Example 1d: Multi-filter for longer Observations
A 28 ks X-ray observation allows four EPIC/RGS Image
mode OM exposures:
1.3 ks + 4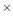 [1.6 ks+(5
[1.6 ks+(5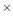 1.0 ks)] = 27.7 ks.
1.0 ks)] = 27.7 ks.
Preferred choice of filters is: U, UVW1, UVM2, UVW2 (in that order).
Due to the different throughput of the different filters
(see Fig. 102), it is recommended to define longer
exposure times for those filters with low throughput. In the above
case, if the U filter is not really needed, one might prefer three
exposures with 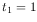 ks,
ks, 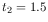 ks, and
ks, and 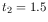 ks, yielding:
ks, yielding:
1.3 ks +
1.6 ks+(5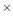 1.0 ks)
1.0 ks)
1.6 ks+(5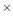 1.5 ks)
1.5 ks)
1.6 ks+(5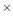 1.9 ks) = 28.1 ks.
1.9 ks) = 28.1 ks.
If only a single filter is to be used, it is better to define only
one exposure with the maximum exposure time of 5 ks:
1.3 ks + 1.6 ks+(5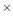 5.0 ks) = 27.9 ks.
5.0 ks) = 27.9 ks.
Example 2: Monitoring a variable point source
It is recommended to use Science User Def mode for variability studies:
define one image window plus one additional fast window, both centred on
the source coordinates. Choose maximum exposure times (4400 sec) to minimise
overhead. The calculation of exposure times is the same as in
example 1a. Depending on the expected time scales of variability,
the time bin size for the fast window can be adjusted to values
between 0.5 and 20 s.
For studies of variability it is recommended to use the same filter for all
observations. While the use of UV filters is encouraged for imaging, it
depends on the scientific aims whether strictly simultaneous X-ray/optical or
X-ray/UV monitoring is of higher interest.
European Space Agency - XMM-Newton Science Operations Centre